式e-4よりVo(t)の最大値は
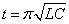 において において
Vo_max = 2Vi・D 式e-5
と求めることができます.よって,ViのPWMパルスのデューティstepの直流成分のみを考えた場合,単純なDC信号のSTEPと全く同様の結果が得られます.ただ,異なる点はこの直流成分の応答にスイッチングによるリップルが加わるということです.式e-5の関係から,本ゲート駆動回路のSW1,SW2のスイッチング・デューティは50%以下に設定することによって前記した1/2の直流電圧を与えた場合と同様の効果が得られオーバーシュートを抑制することができます.
ここまでは,ILg連続領域の話です.常にILg連続の状態の場合,式e-4によると
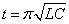 を電圧のIGBTゲートのピークとしてその後, を電圧のIGBTゲートのピークとしてその後,
Vo(2π√(LC)) = 0に向かってIGBTゲート電圧が低下していきます.しかし,本ゲート駆動回路の場合には異なります.Viに相当する電圧は,SW1オン時のB1電圧と,SW2オン時の0Vと,さらにSW1,SW2オフ時のハイ・インピーダンスの3stateの状態になるため(寄生ダイオード通電時もオンとする),SW1,SW2オフ時のハイ・インピーダンスの状態ではILg不連続の領域になります.
すると,Vi PWMパルス・デューティDのSTEP応答の場合には
Vo ≦ Vi・D 式e-6
の状態においてはILgが連続となり,
Vo > Vi・D 式e-7
の状態においてはILgは不連続となります.
このことから実機においては式e-6の条件では,方法2によりゲート駆動され,式e-7の条件では方法1によるゲート駆動となります.このようにIGBTゲートに与える充放電方法を外部要因の動きによって自動的に切りかえることになります.ということで外部因子の挙動を制御側がフィードバックすることなく回路の自然な特性を利用してシンプルなゲート駆動システムを実現できることになります.
SW1,SW2のスイッチング周波数の設定について触れておきます.本ゲート駆動回路の場合,LCの共振周波数よりも充分大きい周波数が要求されますが,実際スイッチング周波数の大きさにともなってSW1,SW2のスイッチング損失が大きくなり,省電力のメリットが目減りします.そこでLCの共振周波数よりも大きい範囲でなるべく小さいスイッチング周波数を設定する必要があります.一般に制御機器におけるスイッチング周波数は制御周波数の1[decade](10倍)以上大きい周波数に設定します.
このゲート駆動回路の場合は,仕様としてオーバーシュートをどれくらい見込めるのかといったところから,実機ベースでテストを重ねスイッチング周波数を極力低く設定することが望ましいと考えています.
|