|
n次系伝達関数の一般式を次の式2-3-40としたとき,この伝達関数の発散・収束,振動について考えます.
|
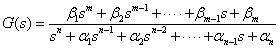 |
式2-3-40 |
|
|
式2-3-40を部分分数に分解します.(部分分数についてはこちらを参照)
|
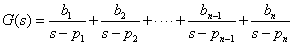 |
式2-3-41 |
|
|
式2-3-41のpxは伝達関数G(s)の極になります.この伝達関数G(s)の単位インパルス応答から特徴を考えます.式2-3-41からインパルス過渡応答を導くと,ラプラス変換表(表2-1-3のNo.4)より
|
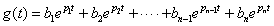 |
式2-3-42 |
|
|
式2-3-42のように eの指数関数になります.ここで,pxは一般に複素数です.pxを次のように置くと px=σx+jωx
式2-3-42は
|
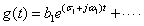 |
式2-3-43 |
|
|
ここで極 pの実数部σに着目すると,t
→ ∞で
σx >
0 で発散
σx < 0 で収束
σx = 0 で無減衰
の特徴が分かると思います.
続いて,振動について考えます.振動はインパルス応答過渡関数にsinなど振動要素が含まれます.
そこで,先に説明した2次系伝達関数と振動の関係を応用していきます.式2-3-41について,ある2点の極
pk,pl(の項)を使って2次系伝達関数の要素を次のように抽出していきます.
|
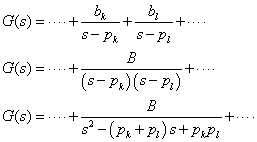
|
|
この式を次のように置くと.
|
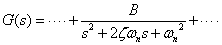 |
式2-3-44 |
|
|
このように2次系伝達関数を伝達関数G(s)に含めて重ね合わせとして考えることができ,2次系伝達関数の特徴(極位置またはζと振動との関係)を踏まえて考えることができます.詳細はすでに説明していますのでこちらを参照.
|
← 戻る 1
2 次へ →
|
単位インパルス応答は,-∞〜+∞[rad/s]の範囲の余弦波(振幅1)を均一に合成した関数であるため,インパルスの過渡応答関数が得られれば,-∞〜+∞[rad/s]の範囲の余弦波のそれぞれの過渡応答の合成波形が得られることになり,伝達関数の物理的な特徴をとらえることができます.
|