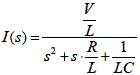式2-1-26

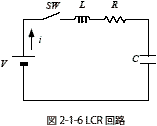式2-1-26は図2-1-6のＲＬＣ回路における過渡電流です．先に式2-1-6の逆ラプラス変換をラプラス変換表（表2-1-3）の４（下表）を用いて解きましたが，別解があるのでそれを示します．

ラプラス変換表（表2-1-3）の７に適合させて変換します．

No	f(t)	F(s)
４	eat
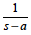７	ebtsin at

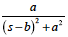表2-1-3抜粋

式2-1-26の分母を(s-b)²+a²の形をつくります．すると

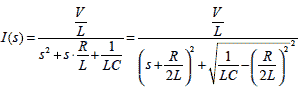式2-1-37

これをラプラス逆変換すると

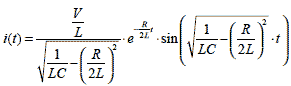式2-1-38

と求めることができましたが，先に部分分数によって求めた式2-1-35とはちょっと異なる形に見えます．しかし，数学ですので解く方法が違っても解は等しくなることが必須ですので数学的に式2-1-38と式2-1-35が等しいことを解説します．

式2-1-38についての解説

式2-1-38のsinについて複素数に展開していきます．e±jθ=cosθ±jsinθより

これを式2-1-38に代入して

よって

式2-1-39

数学的に式2-1-35と式2-1-38は全く同じになります．

← 戻る  1  2  次へ →

▲ページの先頭へ