2次系伝達関数の過渡関数の導出 |
| 単位インパルス応答関数は伝達関数そのものなので
|
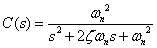
|
| これをラプラス変換表(表2-1-3)No.7に適合させていきます.下表はその抜粋
|
| No |
f(t) |
F(s) |
| 7 |
ebtsin
at |
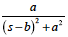 |
|
|
表2-1-3抜粋
分母を(s-b)2+a2の形に変形すると
|
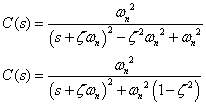
|
| ラプラス変換表より,過渡関数は,
|
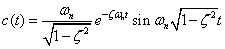 |
式2-3-36 |
|
|
物理解は虚数を含まないので |ζ|<1
が式2-3-36の条件となります.
|
|
| つづいて,ζ<0以外の条件における解をもとめます.
オイラーの関係式(e±jθ=cosθ±jsinθ)より
|
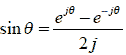
|
| なので式2-3-36は
|
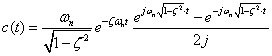
|
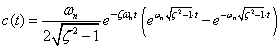 |
式2-3-37 |
|
| ただし条件は
|ζ|>1
|
つづいてζ=1について
単位インパルス応答関数にこの条件を代入すると
|
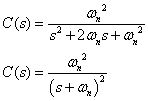
|
| これをラプラス変換表(表2-1-3)No.11に適合させて変換すると
|
| No |
f(t) |
F(s) |
| 11 |
teat |
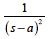 |
|
|
表2-1-3抜粋
|
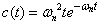 |
式2-3-38 |
|
| 条件は
ζ=1
|
|
|
|