伝達関数は次の式2-3-15のように入出力ラプラス関数の比として与えられることを述べました(式2-3-7参照).
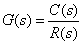 |
式2-3-15 |
このセクションでは,この比に着目していきます.
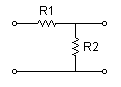
まず,図2-3-13は入出力の信号の関係を単純に比例する回路として示しています.
| R(s) → |
 |
→ C(s) |
図2-3-13 入出力信号を比で示せる回路例
図2-3-13の場合,入力関数r(t)と出力関数c(t)は式2-3-16のような関係があります.
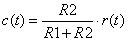 |
式2-3-16 |
図2-3-13の回路の入出力の関係を伝達関数によって示した場合 (式2-3-16から式2-3-17への計算は両辺ラプラス変換し,C(s),R(s)の比より)
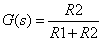 |
式2-3-17 |
この例ように,入出力が抵抗等によって単に比として示せる場合,伝達関数も,式2-3-16の時間関数における比と全く同じ値になります.
一般に伝達関数はラプラス関数によって示されますが,本質的にはここで例示した入出力の比と同次元(物理量に置き換えて言うと単位)の要素になります.また,比は一般にゲイン,利得と言います.
これを踏まえて,先述のRCフィルタ回路(下図)の伝達関数について,比という観点から考えて見ましょう.
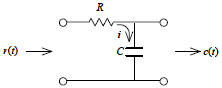 |
伝達関数
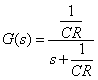 式2-3-18 式2-3-18 |
図2-3-14 RCフィルタ回路と伝達関数
式2-3-18をフーリエ変換して周波数関数を求めると(ラプラス関数のフーリエ変換はこちらを参照)
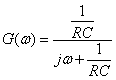 |
式2-3-19 |
この周波数関数をグラフに示すと
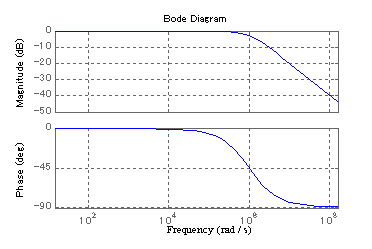
条件:
R=1[Ω]
C=1[μF]
|
図2-3-15 RCローパスフィルタのBode線図
伝達関数の周波数関数は,伝達特性を周波数を引数とした入出力の比として示していることが分かると思います.
伝達関数の周波数関数を,横軸に周波数(角周波数),縦軸にゲイン(入出力の比)として示す図2-3-15のようなグラフをBode線図といいます.
【質問】2008/07/24
FFT-Analyserで伝達関数を測定したのですが、キャリブレーションモードをdBで行い、その時に、レファレンスバリューを
5.00E-08EUから2.00E-05EUに変えても結果は一緒でした。
レファレンスバリューは関係ないのですか?また、何故ですか?
【回答】2008/07/24
測定器関係で困ったら,まずは直接 測定器メーカに電話で問い合わせてみてください.メーカの方は親切に教えてくれますよ.
一般に,デジタル処理を施した測定器は,もはやアプリケーション・ソフトなんです.ですから,考えてわからないものも多いので,
できるだけ時間をかけずに,聞いてしまった方がよいと私は思います.
問い合わせのポイントは,
1.測定機器の型番
2.具体的な(簡単な)測定事案を仮定
3.期待するアウトプット
上の情報が揃えば,このボタンで〜して,〜モードに設定して・・・・みたいに,How toで教えてくれますよ.
また,測定器に付随した付加価値機能や,それに付随する名称は,メーカに聞く以外に解決することはありませんので.
臆することなく確認のみかと.一般に,一流のエンジニアほど外部への確認の頻度は高く怠りませんよ,
どうぞ自信を持って確認されることをおすすめします.
|