つづいてcos波,sin波のについてフーリエ変換をしてみましょう.まずcos波について次の時間関数を例題にフーリエ変換します.
 |
f (t )=cos(ω0t ) |
(-T≦t≦T
) |
| 0 |
(t<-T,
t>T
) |
|
式2-2-23 |
フーリエ変換の定義式は次の通りです.
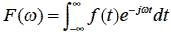 |
式2-2-20 |
式2-2-20に式2-2-23を代入すると
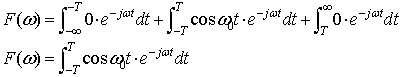
cos(ω0t )はオイラーの関係式より
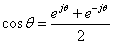
なので
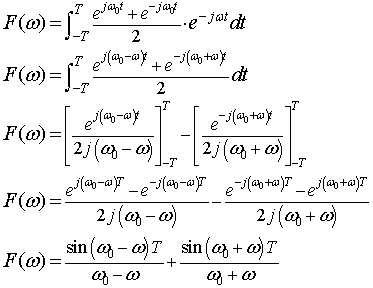
式2-2-24
式2-2-24をグラフに示すと
|
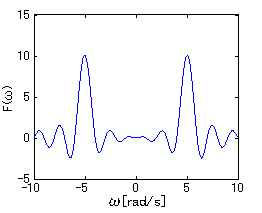
図2-2-4 余弦波のフーリエ変換 |
条件:
T=10s
ω0=5rad/s
|
つづいてsin波について次の時間関数を例題にフーリエ変換します.
 |
f (t )=cos(ω0t ) |
(-T≦t≦T
) |
| 0 |
(t<-T,
t>T
) |
|
式2-2-25 |
式2-2-25をフーリエ変換定義式(式2-2-20)に代入すると
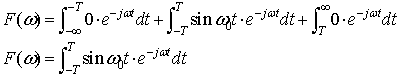
sin(ω0t)はオイラーの関係式より
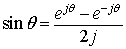
なので
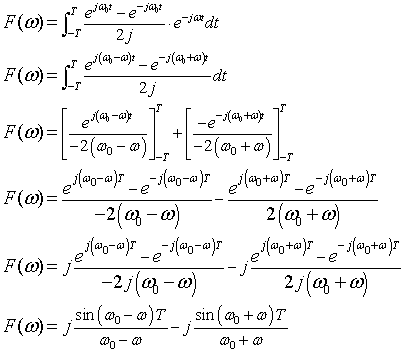 式2-2-26 式2-2-26
式2-2-26をグラフに示すと
|
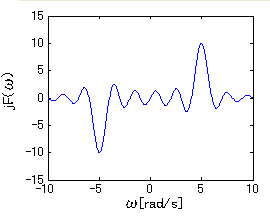
図2-2-5 正弦波のフーリエ変換 |
条件:
T=10s
ω0=5rad/s
|
← 戻る 1
2 3 次へ →
|
|