2枚の絶縁された同一の極板が平行に設置されているとき,その極板にプラスとマイナスの同量の電荷をそれぞれ帯電させると,電界セクション(電界1,2,3)で詳細に示したように,極板と垂直方向に電界が(電気力線が平行に)均一につくられます.
この電気力線が垂直につらぬく平面を想定するとき,この平面上は同電位となります.それは,極板にはさまれた空間は電界の大きさが均一であるためです.
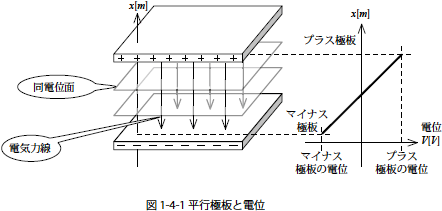
一般に電界の大きさは距離に対する電位の勾配(1)を示します,そのため,この電界(電気力線)に垂直な電位面は電気力線の方向に進むにしたがって電位が低くなる特徴があります.
よってマイナス電荷の帯電している極板はマイナスの電位をもち,プラス電荷が帯電している極板はプラスの電位をもち,両極板間には電位差が存在することがわかります.
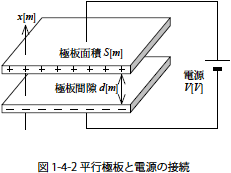
| 逆に,上記の2枚の平行極板に,電気的に中性である状態から図1-4-2 のように直流電源を接続して極板に電位差を与える場合を考えます.
最初2枚の極板は電気的に中性であるため電位差はありません.次に電源が接続されることによって,電荷が運ばれ,極板間の電位差は電源電圧と同電圧になります. |
|
このとき2枚の極板は電源を介した環状の接続なので,それぞれの極板に対して,流出する電荷,または流入する電荷は等しくなります.そしてそれぞれの極板には同量の電荷が異なる極性で充電されます.このような仕組みで電荷を充電できる装置をコンデンサ(2) といいます.
このとき充電される電荷は,極板内の電界の大きさに比例することを先に説明しました(電界セクション参照).そこで極板面積,極板間隙などの条件が同一である場合,電界の大きさと電位差は比例関係にあるので,充電電荷と極板間に与える電圧も比例関係にあることがわかります.
その関係をそれぞれの極板の帯電電荷を+Q,-Q[C] とすると式1-4-2 のように示すことができます.

比例定数であるC は静電容量といいます.コンデンサの電荷の貯め易さを示すパラメータです.単位はファラド[F] を使います.
(1) 電位勾配:
電界の大きさE は次の関係があります.
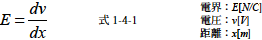
(2) コンデンサ:
コンデンサは2枚の極板によって構成されます.コンデンサに帯電される電荷は,コンデンサを構成する片方の極板だけを考えると,同種(プラス同士またはマイナス同士)の電荷が集まっているので電荷同士に斥力(反発力)が働きます.すると仮に,片方の極板だけに電荷を充電する場合,充電電荷量に対して充電エネルギーが大く必要になるため充電効率がわるいと言えます.ところが2枚の極板を近距離に配置することで,極板間に互いに異種の電荷同士(プラスとマイナスの電荷)に引力が作用します.この引力によって極板に帯電する同種の電荷同士の斥力を相殺することができます.この引力と斥力の作用によって,コンデンサは比較的小さな充電エネルギーでも,大きな電荷量を充電することができます.
|