フーリエ級数のセクションでは，周期関数について直流成分，sin とcos の要素に分解して抽出してきました．ここではそれらの要素を複素数を使うことで統一したパラメータで表現します．

次に示す数式は，複素数によるフーリエ級数展開とフーリエ係数です．

フーリエ級数展開	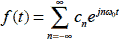式2-2-7
フーリエ係数	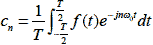式2-2-8

ただし n=・・・-2，-1，0，1，2・・・

ここでc_nを（複素）スペクトルと言います．式2-2-8によって求められるスペクトルは周波数成分の大きさの他，位相情報も含みます．

式2-2-7　複素フーリエ級数について解説

三角関数を用いたフーリエ級数およびフーリエ係数（フーリエ係数の解説はこちら参照）は次式のように与えられます．

フーリエ級数展開 式2-2-1 フーリエ係数 式2-2-2

ここで上式2-2-1 の式中に含むsin およびcos をオイラーの関係式を使って示します．まず，オイラーの関係式は次の次の通り．

式2-2-9

この関係をフーリエ級数（式2-2-1）に代入すると

ここで

ただし n=1，2，3，・・・ 式2-2-10

とcnをおきます．すると

式2-2-11

と示せます． さらに，ここでc0を とおき，さらにn の範囲を負の領域に広げ，n = ・・・-2，-1，0，1，2 ・・・とすることで，式2-2-11に含む２つのΣ を統合すると

ただし n=・・-2，-1，0，1，2・・ 式2-2-12

と示すことができます．

式2-2-8 複素フーリエ係数について解説

つづいてフーリエ係数の関係式（式2-2-2）（an，bn）からcnを求めていきます．まず，式2-2-10に式2-2-2を代入すると

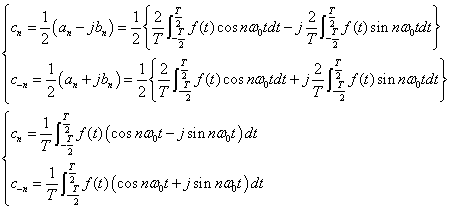
ここでオイラーの関係式

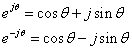
より

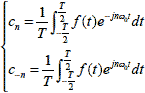ただし n=1，2，3，・・・ 式2-2-13

ここで，nの範囲を負の領域に広げ，n=1，2，3，・・・から n=・・・-2，-1，0，1，2・・・として，式2-2-13の両式を統合することができます． すると cnは

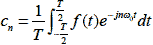ただし n=・・-2，-1，0，1，2・・ 式2-2-14

と示すことができます．

▲ページの先頭へ