導体に電圧を与えると導体内に電界がつくられます.その電界によりキャリアは電気力を受け移動し電流が流れます.移動キャリアの速度は,多くの場合電界の大きさに比例(1) します.このとき導体を流れる電流はキャリアの電荷密度やキャリアの移動し易さに応じた導体固有のパラメータによって決まります.このパラメータをσ とし,単位面積あたりに流れる電流(電流密度(2))をJ とすると式1-2-1 のような関係になります.
| J=σE |
式1-2-1 |
電流密度:J[A/m]
導電率:σ[S/m]
電界:E[N/C]
|
式1-2-1 におけるσ は導電率(3) といいます.導電率は導体の単位体積あたりの電流の流れ易さを示す尺度です.単位は[S/m] を使います.単位のS は“ジーメンス”と読みます.
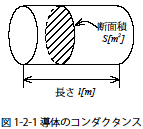
つぎに図1-2-1 の形状をもつ導体の電流の流れ易さを求めます.電流の流れ易さはコンダクタンスという尺度を用いて示します.コンダクタンスをG とした場合,式1-2-2 のようになります.
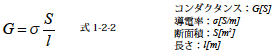
コンダクタンスは電流の進行方向の距離l[m] に反比例し,断面積S[m2]に比例関係があります.
つづいて,導電率,コンダクタンスのように電流の流れ易さを示す尺度に対して電流の流れ難さを示す尺度もあります.単位体積あたりの電流の流れ難さは抵抗率といいます.また電流の流れ難さは抵抗といいます.抵抗率をρ,抵抗をR とすると式1-2-3,式1-2-4 のような関係があります.
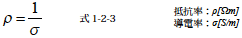

抵抗率の単位は[Ωm],また抵抗の単位は[Ω] を使います.単位のΩ は“オーム”と読みます.図1-2-1 の導体について抵抗を求めると式1-2-5 となります.
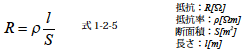
抵抗は電流の進行方向の距離l [m] に比例し,断面積S[m2] に反比例の関係があります.導体における電気特性を示す抵抗とコンダクタンスは本質的には同一の物性を示します.どちらの尺度を用いても電気特性を示すことができるため必要に応じて使い分けられます.電子回路設計の分野では抵抗や抵抗率を用いることが一般的です.電子回路製品には固定抵抗値を持った電子部品(抵抗器)を実装して使用されます.
|
|
解説 |
(1) キャリア速度は電界に比例:
導体中で自由電子などのキャリアが移動する速度は弱電界において電界の大きさに比例します.自由電子の平均速度は式1-2-6 のような比例関係があります. |
| v=μE |
式1-2-6 |
自由電子の平均移動速度:v[m/s]
移動度(導体による比例定数):μ[m2/s/V]
電界:E[N/C] |
|
(2) 電流密度:
電流密度は単位面積あたりの電流を示します.電流は単位時間あたりの電荷移動量ですので式1-2-7 のようになります. |
| J = nQv |
式1-2-7 |
単位体積あたりのキャリア数:n[個/m3]
電流密度:J[A/m]
自由電子の平均移動速度:v[m/s]
キャリア電荷:Q[C] |
|
(3) 導電率:
導電率σ は式1-2-1,式1-2-6,式1-2-7 より式1-2-8 が得られます. |
| σ=nQμ |
式1-2-8 |
単位体積あたりのキャリア数:n[個/m3]
導電率:σ[S/m]
移動度(導体による比例定数):μ[m2/s/V]
キャリア電荷:Q[C] |
|
|